Teorema de Tales.

De acuerdo a unas modificaciones en el temario del 3er trimestre de la materia Matematica, se ha agregado un tema nuevo.
El Teorema de Tales:

Existen dos teoremas que reciben el nombre de Teorema de Tales, ambos atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

[editar] Primer teorema

Una aplicación del Teorema de Tales.

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:

Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.

[editar] Corolario

Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.

Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:

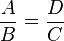
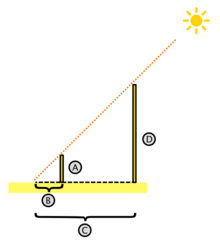
Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la pirámide de Keops en Egipto. En cualquier caso, el teorema per se demuestra la semejanza entre dos triángulos, no la constancia del cociente entre sus lados.

[editar] Segundo teorema

Ilustración del enunciado del segundo teorema de Tales de Mileto.

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:

Sea C un punto de la circunferencia de diámetro [AB], distinto de A y de B. Entonces el ángulo , es recto. Tales de Mileto

Este teorema es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.

Demostración: OA = OB = OC = r, siendo O el punto central del círculo y r el radio de la circunferencia. Por lo tanto y son isósceles. La suma de los ángulos del triángulo ABC es equivalente a 2α + 2β = π (radianes). Dividiendo por dos, se obtiene: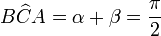
(o 90º).

Además, la bisectriz de un triángulo corta al lado opuesto del ángulo con la bisectriz en dos segmentos iguales. Hipotenusa² = C² + C², es decir AB²=CA²+CB².

En conclusión se forma un triángulo rectángulo.